第 7 章　函數的平移、伸縮與變化¶

本章重點：

  • 理解圖形平移：$y = f(x) + k$, $y = f(x-h)$ 對圖形的影響。
  • 理解圖形伸縮：$y = a f(x)$（垂直）、$y = f(bx)$（水平）的效果。
  • 了解反射：$y = -f(x)$、$y = f(-x)$ 的圖形對稱關係。
  • 以參數控制圖形形狀，觀察參數變化和函數圖形之間的關係。
  • 使用 SymPy/ Python 動手實驗各種變換，培養「看式子想圖形、看圖形猜式子」的能力。

這些技巧在高中課程中常被用來快速畫出新的圖形，也是在微積分中理解「函數族」與模型調整的重要工具。

7.1 基本準備：以 $f(x) = x^2$ 為例¶

在本章中，我們多半會以一個簡單的基礎函數 $f(x) = x^2$ 或 $f(x) = \sin x$ 作為例子，然後對它做各種變換。

先在 SymPy 中定義：

In [1]:
import sympy as sp
sp.init_printing()

x = sp.symbols('x', real=True)
f = x**2
f
Out[1]:
$\displaystyle x^{2}$

接著，可以畫出其圖形（在支援 sp.plot 的環境中）：

In [2]:
sp.plot(f, (x, -4, 4), title='y = x^2')
No description has been provided for this image
Out[2]:
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7fe218b5da90>

7.2 垂直平移：$y = f(x) + k$¶

若已知 $y = f(x)$ 的圖形，則：

  • $y = f(x) + k$ 會把整個圖形向上平移 $k$ 個單位（若 $k>0$）。
  • 若 $k<0$，則向下平移 $|k|$ 個單位。

例：以 $f(x)=x^2$ 為例，考慮 $g(x) = x^2 + 2$。

In [3]:
g = f + 2
sp.plot(f, g, (x, -4, 4), legend=True, title='y = x^2 and y = x^2 + 2')
No description has been provided for this image
Out[3]:
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7fe21691e990>

你可以觀察到兩條拋物線的形狀完全一樣，只是其中一條向上平移了。

7.3 水平平移：$y = f(x-h)$¶

這個部分常讓人混淆：

  • $y = f(x-h)$：圖形向右平移 $h$（若 $h>0$）。
  • $y = f(x+h)$：圖形向左平移 $h$。

例：以 $f(x) = x^2$ 為例，考慮 $g(x) = (x-2)^2$。

In [4]:
g_shift = (x-2)**2
sp.plot(f, g_shift, (x, -1, 5), legend=True, title='y = x^2 and y = (x-2)^2')
No description has been provided for this image
Out[4]:
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7fe216891310>

這裡 $y=(x-2)^2$ 是把原本的拋物線向右平移 2 個單位。 你可以試著改成 $(x+2)^2$，看看圖形會向哪邊移動。

7.4 垂直伸縮與反射：$y = a f(x)$¶

給定 $y=f(x)$，若考慮 $y = a f(x)$：

  • 若 $|a|>1$，圖形會沿著 $y$ 軸方向「拉長」，變得更窄（拋物線例子）。
  • 若 $0<|a|<1$，圖形會「壓扁」，變得更寬。
  • 若 $a<0$，圖形會相對於 $x$ 軸上下翻轉（反射）。

以 $f(x)=x^2$ 為例，畫出 $y = x^2$、$y = 2x^2$、$y = \frac{1}{2}x^2$：

In [5]:
sp.plot(x**2, 2*x**2, sp.Rational(1,2)*x**2,
        (x, -4, 4), legend=True,
        title='y = x^2, 2x^2, (1/2)x^2')
No description has been provided for this image
Out[5]:
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7fe2167aa5d0>

再看看 $y = -x^2$ 的情況：

In [6]:
sp.plot(x**2, -x**2, (x, -4, 4), legend=True, title='y = x^2 and y = -x^2')
No description has been provided for this image
Out[6]:
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7fe2166c3b10>

7.5 水平伸縮與反射：$y = f(bx)$¶

給定 $y = f(x)$，考慮 $y = f(bx)$：

  • 若 $|b|>1$，圖形在水平方向被壓縮（變窄）。
  • 若 $0<|b|<1$，圖形在水平方向被拉寬。
  • 若 $b<0$，圖形相對於 $y$ 軸左右翻轉（反射）。

這點常與垂直伸縮混淆，可以透過例子加深印象。

例：以 $f(x) = \sin x$，比較 $\sin x$ 與 $\sin(2x)$、$\sin(\frac{x}{2})$。

In [7]:
f_sin = sp.sin(x)
sp.plot(f_sin, sp.sin(2*x), sp.sin(x/2),
        (x, -2*sp.pi, 2*sp.pi), legend=True,
        title='sin(x), sin(2x), sin(x/2)')
No description has been provided for this image
Out[7]:
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7fe216474e10>

你會發現：

  • $\sin(2x)$ 的波形在 $x$ 軸上「擠」在一起（週期變為原來的一半）。
  • $\sin(\frac{x}{2})$ 的波形被拉長（週期變為原來的兩倍）。

7.6 綜合變換：$y = a\, f(b(x-h)) + k$¶

一般來說，我們可以把各種變換組合在一起，形成：

$y = a\, f(b(x-h)) + k$。

  • $h$：控制水平平移（右移 $h$）。
  • $k$：控制垂直平移（上移 $k$）。
  • $a$：控制垂直伸縮與上下反射。
  • $b$：控制水平伸縮與左右反射。

例：以 $f(x) = x^2$，考慮：

$g(x) = -2\, (x-1)^2 + 3$。

這代表：

  • 將基礎拋物線 $x^2$ 向右平移 1。
  • 垂直方向放大 2 倍並上下翻轉。
  • 再向上平移 3。

我們可以畫出 $y = x^2$ 與 $y = -2(x-1)^2 + 3$：

In [8]:
g = -2*(x-1)**2 + 3
sp.plot(x**2, g, (x, -3, 5), legend=True,
        title='y = x^2 and y = -2(x-1)^2 + 3')
No description has been provided for this image
Out[8]:
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7fe219099450>

試著改變係數與常數（例如改成 -1/2、+1 等），觀察圖形如何變化， 逐漸建立「看式子就能 roughly 想到圖形長相」的能力。

7.7 參數動畫的概念（文字說明）¶

在 Jupyter Notebook 中，有時會搭配 ipywidgets 做參數滑桿， 讓你可以動態調整 $a, h, k$ 等參數並即時看到圖形變化。

下面提供一個基礎框架（需先安裝 ipywidgets）：

In [9]:
# 以下程式在支援 ipywidgets 的環境中可使用
from ipywidgets import interact

def plot_quadratic(a=1.0, h=0.0, k=0.0):
     x = sp.symbols('x')
     f = a*(x-h)**2 + k
     sp.plot(f, (x, -10, 10), ylim=[-10, 10])

interact(plot_quadratic, a=(-3, 3, 0.5), h=(-5, 5, 1), k=(-5, 5, 1));

interactive(children=(FloatSlider(value=1.0, description='a', max=3.0, min=-3.0, step=0.5), IntSlider(value=0,…

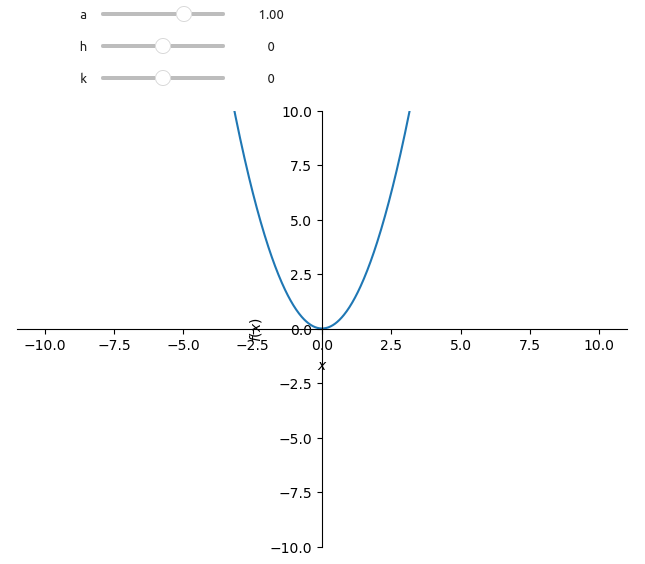
若無法使用互動工具，也可以手動改動參數、多畫幾張圖， 效果同樣是訓練你對「參數 → 圖形」之間關係的直覺。

7.8 啟發性例子一：音樂中的頻率與 $\sin(bx)$¶

在聲音與音樂中，純音可近似為正弦波：$A\sin(\omega t)$， 其中 $\omega$ 與「頻率」有關。

  • 當 $\omega$ 變大，波形在時間軸上被「擠」在一起，聲音的頻率變高（音調變高）。
  • 當 $\omega$ 變小，波形被「拉長」，頻率變低（音調變低）。

這與我們在本章看到的 $y = \sin(bx)$ 水平伸縮變換相同。

以下用 SymPy 畫出不同頻率的正弦波（把 $x$ 當作時間 $t$）：

In [10]:
sp.plot(sp.sin(x), sp.sin(2*x), sp.sin(4*x),
        (x, 0, 2*sp.pi), legend=True,
        title='Sine waves of different frequencies: sin(x), sin(2x), sin(4x)')
No description has been provided for this image
Out[10]:
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7fe214b53c50>

你可以聯想到：

  • $\sin(x)$：基準音。
  • $\sin(2x)$：頻率加倍（高一個八度的感覺）。
  • $\sin(4x)$：頻率再加倍。

這樣，數學中的「水平伸縮」就與生活中的聲音高度直接關聯起來。

7.9 啟發性例子二：影像亮度調整與垂直變換¶

在影像處理中，灰階影像的每個像素有一個亮度值（例如 0 ~ 255）。 如果我們把亮度視為函數 $I(x)$ 的輸出，則：

  • 讓整體變亮：$I_{new}(x) = I(x) + c$（垂直平移）。
  • 增加對比：$I_{new}(x) = a I(x)$（垂直伸縮）。

雖然我們這裡不直接處理影像，但可以用簡單的函數模擬： 假設某條亮度曲線 $L(x) = 50 + 20\sin x$，調亮 30 的效果是 $L_{new}(x) = L(x) + 30$。

In [11]:
L  = 50 + 20*sp.sin(x)
Ln = L + 30
sp.plot(L, Ln, (x, 0, 2*sp.pi), legend=True,
        title='Brightness Curve: Original and Increased Brightness')
No description has been provided for this image
Out[11]:
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7fe214a4e490>

雖然實際影像是二維的，但這個一維例子讓我們看到： 圖形的垂直平移與伸縮在各種調整「輸出值」的應用中都扮演相似角色。

7.10 啟發性例子三：統計中的標準化（平移 + 伸縮）¶

在統計學中，我們常常要把一組資料 $X$ 轉換成「標準化」的變數 $Z$：

$Z = \dfrac{X - \mu}{\sigma}$，

其中 $\mu$ 是平均數，$\sigma$ 是標準差。

這其實就是：

  1. 先做水平平移（在隨機變數軸上視角）：減去平均 $\mu$，
  2. 再做水平伸縮（縮放）：除以 $\sigma$。

如果把某個機率密度函數 $f_X(x)$ 畫出來， 那麼對應的 $Z$ 變數密度函數會經歷「平移 + 伸縮」的圖形變換。

以下用一個簡單的二次函數模型示意：

In [12]:
mu = 1
sigma = 2

f_X = - (x-mu)**2 + 4  # 只是示意用的「山形」函數
z = sp.symbols('z', real=True)
f_Z = f_X.subs(x, sigma*z + mu)  # 將 x = sigma*z + mu 代入

f_X, f_Z
Out[12]:
$\displaystyle \left( 4 - \left(x - 1\right)^{2}, \ 4 - 4 z^{2}\right)$

若在同一張圖上畫出 $f_X$ 與「重新命名後的」$f_Z$，可以看見圖形平移與伸縮後的關係。 雖然嚴格的機率密度還需要正規化等條件，但這個例子讓我們理解： 統計中的標準化，其實就是函數圖形的幾何變換的一種。

7.11 本章小結¶

本章你學到了：

  • $y = f(x) + k$、$y = f(x-h)$ 對圖形的垂直與水平平移效果。
  • $y = a f(x)$、$y = f(bx)$ 對圖形的垂直與水平伸縮與反射效果。
  • 綜合變換 $y = a f(b(x-h)) + k$ 可以表示相當廣泛的圖形變化。
  • 利用 SymPy 繪圖，觀察參數如何改變圖形的形狀與位置。
  • 這些變換在聲音頻率、影像亮度、統計標準化等現實應用中，都扮演類似角色。

若能熟練地在腦中想像「函數變形」的效果，你在後續學習微積分、常微分方程、甚至機器學習模型時， 都會有很大的直觀優勢。

7.12 練習題¶

請在本 Notebook 中新增儲存格，試著完成以下練習：

  1. 垂直平移
    (a) 以 $f(x) = x^2$，畫出 $y = f(x)$ 與 $y = f(x) - 3$。
    (b) 找出兩條拋物線的頂點座標，並說明它們之間的關係。

  2. 水平平移
    (a) 以 $f(x) = x^2$，畫出 $y = f(x)$、$y = f(x-1)$、$y = f(x+2)$。
    (b) 分別寫出這三條拋物線的頂點座標，並描述它們的變化規律。

  3. 垂直伸縮與反射
    以 $f(x) = x^2$：
    (a) 畫出 $y = f(x)$ 與 $y = 3f(x)$，並比較圖形開口的「寬窄」。
    (b) 畫出 $y = f(x)$ 與 $y = -f(x)$，觀察圖形如何相對於 $x$ 軸翻轉。

  4. 水平伸縮（以三角函數為例）
    (a) 畫出 $y = \sin x$ 與 $y = \sin(2x)$，在同一張圖上。
    (b) 找出它們在 $x$ 軸上的週期（相鄰兩個相同點的距離），並比較之。
    (c) 試著畫出 $y = \sin(\frac{x}{2})$，觀察週期如何改變。

  5. 綜合變換
    令 $f(x) = x^2$，考慮 $g(x) = -2(x-1)^2 + 3$。
    (a) 寫出 $g(x)$ 的頂點與開口方向。
    (b) 用程式畫出 $f(x)$ 與 $g(x)$，並用文字解釋：從 $f$ 變到 $g$ 經過了哪些步驟（先平移再伸縮、還是相反？）。

  6. 應用題：音調與正弦波
    (a) 以 $f(x) = \sin x$ 為基準，畫出 $\sin x$ 與 $\sin(3x)$。
    (b) 數一數在 $[0, 2\pi]$ 內各自完成了幾個完整週期。
    (c) 用文字說明「頻率變成 3 倍」如何在圖形上呈現。

  7. 加分題：用眼睛看出變換順序
    觀察兩個函數圖形：$y_1 = x^2$ 與 $y_2 = -\frac{1}{2}(x+1)^2 + 2$（請先用程式畫出）。
    (a) 試著用語言描述：從 $y_1$ 變成 $y_2$ 可以拆成哪幾個簡單步驟（平移、伸縮、反射）。
    (b) 寫下兩種不同的「變換順序」，並用數學式子說明它們其實表示同一個結果。

回首頁